|
返回时间序列的绝对能量,即平方值的总和 |
计算时间序列 x 的最高绝对值。 |
|
返回序列 x 中连续变化的绝对值总和 |
|
|
时间序列自相关的描述性统计。 |
|
计算时间序列值(按块聚合)与从 0 到块数减一的序列的线性最小二乘回归。 |
|
实现向量化的近似熵算法。 |
|
此特征计算器拟合自回归 AR(k) 过程的无条件最大似然估计。 |
|
时间序列是否有单位根? |
|
根据公式 [1] 计算指定滞后的自相关性 |
适用于异常检测应用 [1][2]。返回第一位数字分布的关联性,当 |
|
|
首先将 x 的值分到 max_bins 个等距箱中。 |
|
使用 c3 统计量测量时间序列的非线性 |
|
首先根据 x 分布的分位数 ql 和 qh 确定一个区间。 |
|
此函数计算器是时间序列复杂度的估计 [1](更复杂的时间序列有更多的峰值、谷值等)。 |
|
返回 x 中大于 t 的值的百分比 |
返回 x 中大于 x 的平均值的数量 |
|
|
返回 x 中小于 t 的值的百分比 |
返回 x 中小于 x 的平均值的数量 |
|
|
计算 Ricker 小波(也称为“墨西哥帽小波”)的连续小波变换,其定义为 |
|
计算 N 块中第 i 块的平方和与整个序列的平方和之比。 |
|
返回绝对傅里叶变换谱的谱质心(均值)、方差、偏度和峰度。 |
|
使用快速傅里叶变换算法计算实输入的一维离散傅里叶变换的傅里叶系数 |
返回 x 的最大值的第一个位置。 |
|
返回 x 的最小值的第一个位置。 |
|
|
计算时间序列功率谱密度(使用 Welch 方法)的分箱熵。 |
|
多项式 |
检查 x 中是否有任何值出现多次 |
|
检查 x 的最大值是否出现多次 |
|
检查 x 的最小值是否出现多次 |
|
|
计算时间序列 x 的相对索引 i,其中 x 质量的 q% 在 i 的左侧。 |
|
返回 x 的峰度(使用调整的 Fisher-Pearson 标准化矩系数 G2 计算)。 |
|
时间序列是否有大标准差? |
返回 x 的最大值的相对最后一个位置。 |
|
返回 x 的最小值的最后一个位置。 |
|
|
基于 Lempel-Ziv 压缩算法计算复杂度估计。 |
|
返回 x 的长度 |
|
计算时间序列值与从 0 到时间序列长度减一的序列的线性最小二乘回归。 |
|
计算时间序列值与从 0 到时间序列长度减一的序列的线性最小二乘回归。 |
返回 x 中大于 x 的平均值的最长连续子序列的长度 |
|
返回 x 中小于 x 的平均值的最长连续子序列的长度 |
|
计算一维矩阵剖面 [1],并返回 Tukey 五数概要加上该矩阵剖面的均值。 |
|
从拟合到 Langevin 模型确定性动力学的多项式 |
|
计算时间序列 x 的最高值。 |
|
返回 x 的均值 |
|
第一次差分的平均值。 |
|
时间序列差分的平均值。 |
|
计算时间序列的 n 个绝对最大值的算术平均值。 |
|
返回二阶导数中心近似的平均值 |
|
返回 x 的中位数 |
|
计算时间序列 x 的最低值。 |
|
计算 x 在 m 上的交叉次数。 |
|
x 中不同峰的数量。 |
|
计算时间序列 x 中至少支持 n 的峰的数量。 |
|
计算给定滞后的偏自相关函数值。 |
|
返回非唯一数据点的百分比。 |
|
返回在时间序列中出现多次的值的百分比。 |
|
计算排列熵。 |
|
计算 x 的 q 分位数。 |
|
此特征计算器接受输入查询子序列参数,将查询(在 z 标准化欧几里得距离下)与时间序列中的所有子序列进行比较,并返回在时间序列中找到查询的次数(在某个预定义的最大距离阈值内)。 |
|
计算区间 [min, max) 内的观测值数量。 |
|
距离 x 的均值超过 r * std(x)(即 r 倍标准差)的值的比例。 |
|
返回一个因子,如果时间序列中的所有值只出现一次,则因子为 1;否则,因子小于 1。 |
|
返回时间序列的均方根 (rms)。 |
|
计算并返回 x 的样本熵。 |
|
此方法返回一个装饰器,该装饰器将函数的属性 key 设置为 value |
|
返回 x 的样本偏度(使用调整的 Fisher-Pearson 标准化矩系数 G1 计算)。 |
|
此特征计算器估计时间序列 x 在不同频率下的交叉功率谱密度。 |
|
返回 x 的标准差 |
|
返回在时间序列中出现多次的所有数据点之和。 |
|
返回在时间序列中出现多次的所有值之和。 |
|
计算时间序列值的总和 |
|
布尔变量,表示 x 的分布是否看起来对称。 |
|
返回时间反转不对称统计量。 |
|
计算值 value 在时间序列 x 中的出现次数。 |
|
返回 x 的方差 |
|
方差是否大于标准差? |
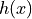 的系数,该多项式已拟合到 Langevin 模型的确定性动力学
的系数,该多项式已拟合到 Langevin 模型的确定性动力学